The final version of our latest paper on: “Observation of Perfect Absorption in Hyperfine Levels of Molecular Spins with Hermitian Subspaces” appeared on Nature Communications: https://www.nature.com/articles/s41467-025-67163-z
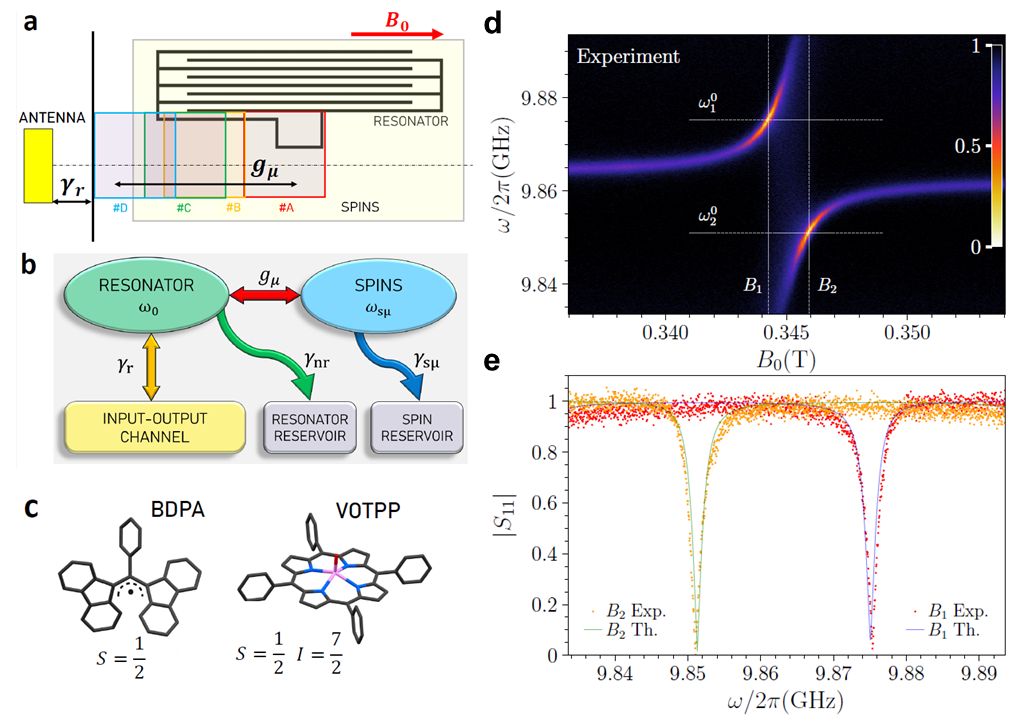
Abstract: “We investigate Perfect Absorption (PA) of radiation, in which incoming energy is entirely dissipated, in a system consisting of molecular spin centers coherently coupled to a planar microwave resonator operated at milliKelvin temperature and in the single photon regime. This platform allows us to fine tune the spin-photon coupling and to control the effective dissipation of the two subsystems towards the environment, thus giving us the opportunity to span over a wide space of parameters. Our system can be effectively described by a non-Hermitian Hamiltonian exhibiting distinct Hermitian subspaces. We experimentally show that these subspaces, linked to the presence of PA, can be engineered through the resonator-spin detuning, which controls the composition of the polaritons in terms of photon and spin content. In such a way, the required balance between the feeding and the loss rates is effectively recovered even in the absence of PT-symmetry. We show that Hermitian subspaces influence the overall aspect of coherent spectra of cavity QED systems and enlarge the possibility to explore non-Hermitian effects in open quantum systems. We finally discuss how our results can be potentially exploited for applications, in particular as single-photon switches and modulators.“
